a)
Mit der Wahrheitstabelle das KV-Diagramm erstellen:
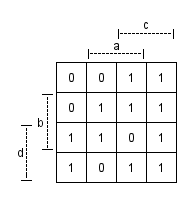
Beispiel:
a, b, c, d = 0 -> f = 0, ist oben links im KV-Diagramm, da ¬a ∧ ¬b ∧ ¬c ∧ ¬d = 0.
b)
Implikanten 0. Ordnung lassen sich leicht aus der Wahrheitstabelle ablesen:
¬a ∧ ¬b ∧ ¬c ∧ d
a ∧ b ∧ c ∧ ¬d
a ∧ b ∧ ¬c ∧ ¬d
¬a ∧ b ∧ ¬c ∧ d
¬a ∧ b ∧ c ∧ ¬d
¬a ∧ b ∧ c ∧ d
a ∧ ¬b ∧ c ∧ ¬d
a ∧ ¬b ∧ c ∧ d
a ∧ b ∧ ¬c ∧ ¬d
a ∧ b ∧ ¬c ∧ d
a ∧ b ∧ c ∧ ¬d
Implikanten 1. Ordnung lassen sich mit dem KV-Diagramm bestimmen:
a ∧ b ∧ ¬d
a ∧ b ∧ ¬c
b ∧ ¬c ∧ d
¬a ∧ ¬c ∧ d
¬a ∧ ¬b ∧ d
¬a ∧ ¬b ∧ c
¬b ∧ c ∧ d
¬a ∧ c ∧ d
¬a ∧ c ∧ ¬d
a ∧ c ∧ ¬d
¬b ∧ c ∧ ¬d
a ∧ ¬b ∧ c
¬a ∧ b ∧ d
Implikanten 2. Ordnung lassen sich mit dem KV-Diagramm bestimmen:
c ∧ ¬d
¬a ∧ c
¬b ∧ c
¬a ∧ d
c)
Insgesamt:
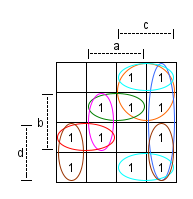
Einzeln:
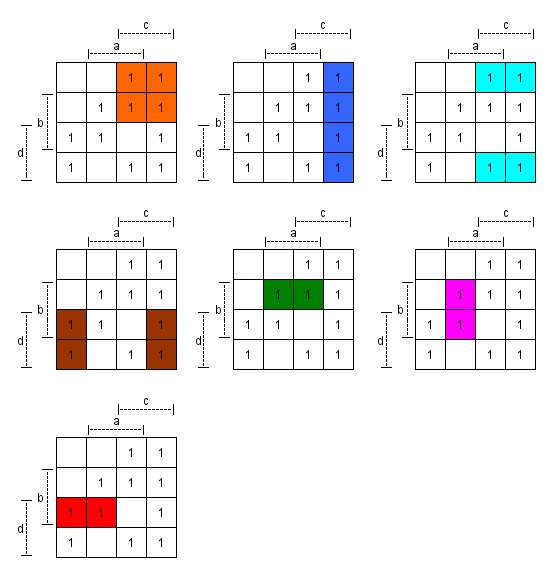
Damit folgende Primimplikanten:
c ∧ ¬d (Orange)
¬a ∧ c (Blau)
¬b ∧ c (Cyan)
¬a ∧ d (Braun)
a ∧ b ∧ ¬d (Grün)
a ∧ b ∧ ¬c (Pink)
b ∧ ¬c ∧ d (Rot)
d)
Insgesamt:
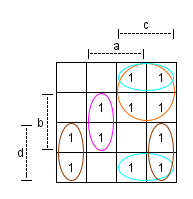
Einzeln:
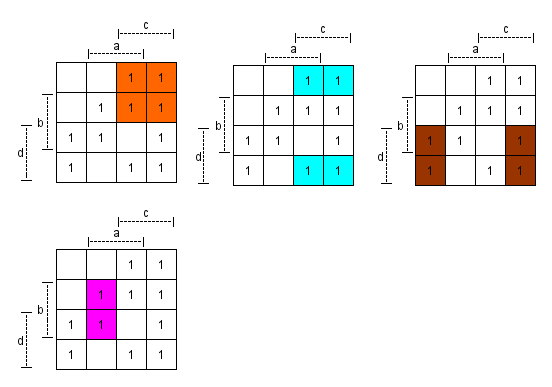
Damit folgende Kernprimimplikanten:
c ∧ ¬d (Orange)
¬b ∧ c (Cyan)
¬a ∧ d (Braun)
a ∧ b ∧ ¬c (Pink)
e)
Kernprimimplikanten mit ODER verknüpfen um DMF zu bilden:
$$f_{DMF}(a,b,c,d) = (c ∧ ¬d) ∨ (¬b ∧ c) ∨ (¬a ∧ d) ∨ (a ∧ b ∧ ¬c)$$
f)
Implikate 0. Ordnung lassen sich leicht aus der Wahrheitstabelle ablesen:
a ∨ b ∨ c ∨ d
a ∨ ¬b ∨ c ∨ d
¬a ∨ b ∨ c ∨ d
¬a ∨ b ∨ c ∨ ¬d
¬a ∨ ¬b ∨ ¬c ∨ ¬d
Implikate 1. Ordnung lassen sich mit dem KV-Diagramm bestimmen:
¬a ∨ b ∨ c
b ∨ c ∨ d
a ∨ c ∨ d
g)
Eine minimale vollständige Überdeckung finden.
Insgesamt:
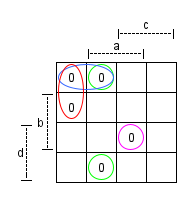
Einzeln:
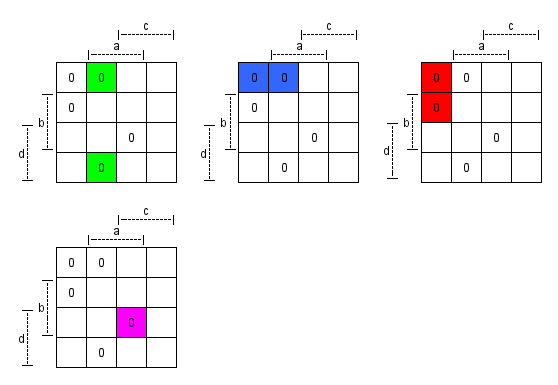
Damit folgende Primimplikate:
¬a ∨ b ∨ c (Grün)
b ∨ c ∨ d (Blau)
a ∨ c ∨ d (Rot)
¬a ∨ ¬b ∨ ¬c ∨ ¬d (Pink)
h)
Eine minimale vollständige Überdeckung finden.
Insgesamt:
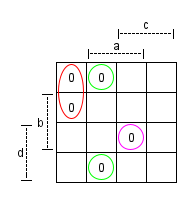
Einzeln:
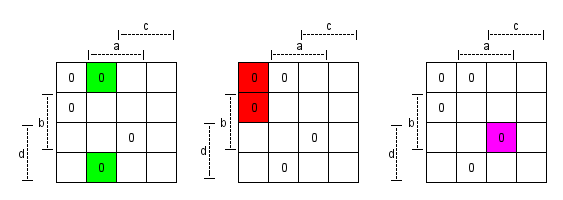
Damit folgende Kernprimimplikate:
¬a ∨ b ∨ c (Grün)
a ∨ c ∨ d (Rot)
¬a ∨ ¬b ∨ ¬c ∨ ¬d (Pink)
i)
Kernprimimplikate mit UND verknüpfen um KMF zu bilden:
$$f_{KMF}(a,b,c,d) = (¬a ∨ b ∨ c) ∧ (a ∨ c ∨ d) ∧ (¬a ∨ ¬b ∨ ¬c ∨ ¬d)$$