
1. Einführung
Wer kennt es nicht? Nach einigen Stunden schweißtreibender Programmierarbeit stellt man beim Testen plötzlich fest, dass sich irgendwo in der Implementierung (mindestens) ein Fehler eingeschlichen haben muss, da das Programm nicht aufhört zu rechnen. Oftmals hat sich in solchen Fällen das Programm in einer sogenannten Endlosschleife verfangen, die (wie der Name bereits vermuten lässt) niemals endet, also unendlich lang der innerhalb des Schleifenrahmens gekapselte Code ausgeführt wird. Ein Programmierer erkennt sofort, dass
int x = 42;
while (x == 42) {
// Do nothing ...
}
System.out.println("Fertig!");
niemals den Text "Fertig!" auf die Konsole drucken wird, da die Bedingung x == 42 immer wahr ist, denn schließlich werden an der Variablen x keine Änderungen vorgenommen. Doch nicht immer ist der Programmcode so leicht zu durchschauen (insbesondere dann, wenn man eine komplexe Anwendung untersucht). Bis heute (Stand: 24.02.2018) ist z. B. nicht bekannt, ob die Collatz-Folge tatsächlich immer bei der \(1\) endet. Der folgende Algorithmus illustriert die Bildung der Collatz-Folge:
public static void collatz_series(int n){
while(n > 1){
if(n%2 == 0){
n/=2; // Teile n durch 2
} else {
n = 3*n+1;
}
System.out.print(n + " ");
}
}
Für die Eingabe n=42 ergibt sich folgender Output:
21 64 32 16 8 4 2 1
Wikipedia sagt zum Collatz-Problem (also genau der Frage, ob die Collatz-Folge nach endlich vielen Schritten mit der \(1\) endet):
Das Collatz-Problem, auch als (3n+1)-Vermutung bezeichnet, ist ein ungelöstes mathematisches Problem [...]
Nun könnte man auf die Idee kommen ein Programm nur lange genug laufen zu lassen, um nach endlicher Zeit sagen zu können "Das Programm hält" oder "Das Programm hält nicht". Dieser Ansatz ist aber offensichtlich nicht zielführend, da man für Programme, die in einer Endlosschleife festhängen (theoretisch) unendlich lange auf ein Ergebnis warten müsste!
Die Frage, ob man für ein Programm \(P\) und eine Eingabe \(E\) feststellen kann, ob \(P\) auf \(E\) hält oder nicht, bezeichnet man als das Halteproblem.
2. Die (scheinbare) Lösung
Als Informatiker liegt die Lösung für dieses Problems auf der Hand: Wir entwerfen einfach einen Algorithmus bzw. bauen eine Maschine, die uns in endlicher Zeit mitteilen kann, ob ein gegebenes Programm bei einer bestimmten Eingabe hält \((1)\) oder nicht hält \((0)\). Diese Maschine sieht folgendermaßen aus:
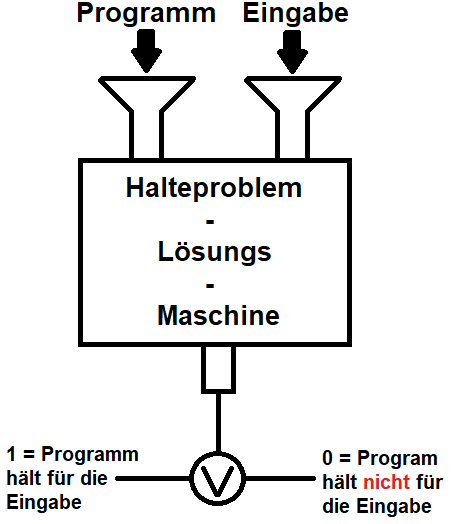
Da alle intuitiv berechenbaren Funktionen genau die Turing-berechenbaren Funktionen sind, handelt es sich bei unserer entworfenen Maschine auch um eine Turing-Maschine. Problem gelöst! Ganz im Stile von Fermat behaupte ich einfach, dass ich einen Algorithmus gefunden habe, der das Halteproblem löst und stelle ihn hier mit einer Blackbox dar. Der Artikel ist an dieser Stelle bereits zu Ende ... oder? Schön wäre es! Man kann logisch begründen, dass so eine Maschine nicht existieren kann und ich mit der Behauptung
"Ich habe einen Algorithmus gefunden, der das Halteproblem löst!"
gelogen habe. Mit solch einer Maschine könnte man zwar etliche Programmierer rund um den gesamten Globus sehr glücklich machen, doch leider stellt die Existenz eines solchen Algorithmus/einer solchen Maschine ein Paradoxon dar. Aber warum?
3. Warum das Halteproblem nicht entscheidbar ist
Nehmen wir an, unsere Turing-Maschine löst das Halteproblem. Dann müsste die Turing-Maschine für das Programm \(P\) mit dem Programm \(P\) als Eingabe auch in endlicher Zeit entscheiden können, ob \(P\) mit \(P\) als Eingabe hält oder nicht.
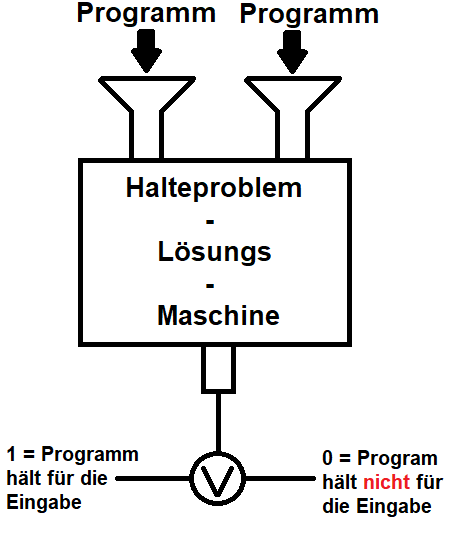
Dass das Füttern der Turing-Maschine mit \(P\) als Programm und Eingabe funktioniert, illustriert die folgende (stark vereinfacht) Skizze einer \(1-\)Band\(-\)Turingmaschine:
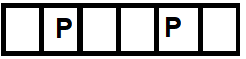
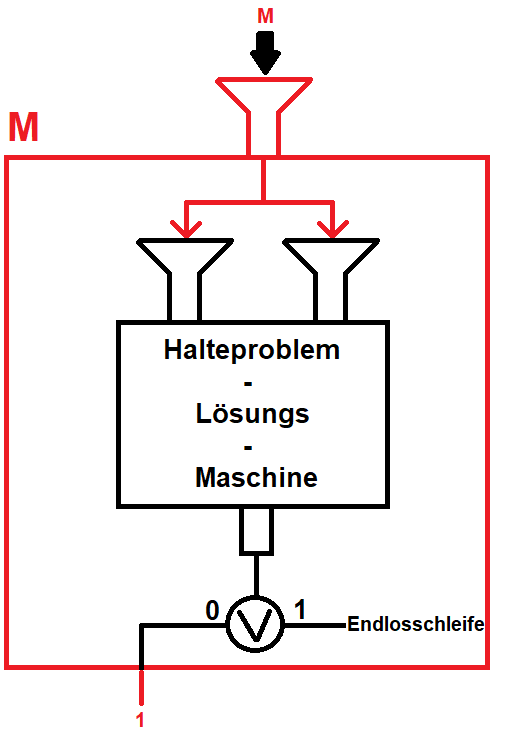
Wir konstruieren nun eine weitere Maschine \(\mathcal{M}\) mit folgendem Aufbau:
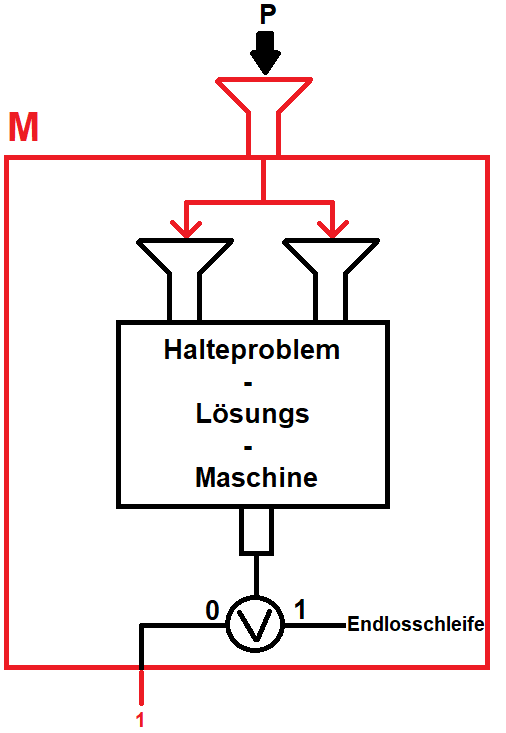
Die Maschine \(\mathcal{M}\) nimmt als Eingabe ein beliebiges Programm \(P\) entgegen und gibt dieses als Programm und Eingabe in unsere Halteproblem-Lösungs-Maschine. Immer dann, wenn unsere Halteproblem-Lösungs-Maschine sagt, dass das Programm nicht hält, geben wir eine \(1\) aus und zeigen so, dass es hält. Andernfalls führen wir das Programm in eine Endlosschleife. Hierbei handelt es sich um ein legitimes Programm, das intern mit dem (uns unbekannten) Code für die Halteproblem-Lösungs-Maschine arbeitet.
So weit das Setup. Jetzt geben wir allerdings den Programmcode unserer so konstruierten Maschine \(\mathcal{M}\) selbst als Input in \(\mathcal{M}\) ein.
Wir unterscheiden nun folgende Fälle:
1.) \(\mathcal{M}\) hält mit der Eingabe \(\mathcal{M}\): Dann gibt unsere Halteproblem-Lösungs-Maschine eine \(1\) aus, was wiederum zu einer Endlosschleife führt, sodass \(\mathcal{M}\) nicht hält. Dies ist aber offensichtlich ein Widerspruch, da wir zuvor angenommen haben, dass \(\mathcal{M}\) mit der Eingabe \(\mathcal{M}\) hält.
2.) \(\mathcal{M}\) hält nicht mit der Eingabe \(\mathcal{M}\): Dann gibt unsere Halteproblem-Lösungs-Maschine eine \(0\) aus und \(\mathcal{M}\) selbst eine \(1\). D. h. \(\mathcal{M}\) hält mit der Eingabe \(\mathcal{M}\). Auch das ist ein Widerspruch, da wir zuvor angenommen haben, dass \(\mathcal{M}\) gerade nicht mit der Eingabe von \(\mathcal{M}\) hält.
Somit ist sowohl die Aussage
\(\mathcal{M}\) hält mit der Eingabe \(\mathcal{M}\)
als auch ihre Negation
\(\mathcal{M}\) hält nicht mit der Eingabe \(\mathcal{M}\)
falsch. So etwas bezeichnet man als Paradoxon. Daraus können wir schlussfolgern: Eine Halteproblem-Lösungs-Maschine kann es nicht geben, denn wir haben zuvor angenommen, dass es solch eine (Turing-)Maschine gibt, was wiederum zu diesem Widerspruch geführt hat! Das Halteproblem ist demnach nicht entscheidbar.
Ganz ähnlich ist übrigens auch die Argumentation beim Barbier-Paradoxon https://de.wikipedia.org/wiki/Barbier-Paradoxon oder die Frage, ob das Wort "heterologisch" selbst ein heterologisches Wort ist.
4. Fazit
Das Halteproblem ist nicht entscheidbar. Es ist allerdings semi-entscheidbar. Was der Unterschied zwischen Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit ist, werden wir in einem anderen Stack-Artikel zur "Theoretischen Informatik" näher untersuchen.
Übrigens
Das folgende Video illustriert auf mehr oder weniger unterhaltsame Art und Weise das Halteproblem:
https://www.youtube.com/watch?v=92WHN-pAFCs
Autor: Florian André Dalwigk
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.