Diesen Artikel gibt es auch auf: https://www.cyber-sicherheit.online/diffie-hellman-schlüsselaustausch/

1. Einführung
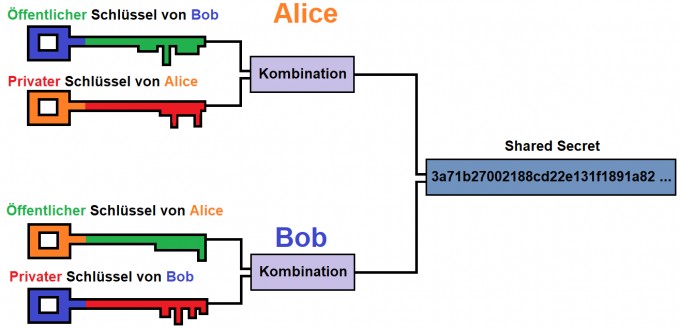
Whitfield Diffie und Martin E. Hellman haben 1976 in diesem Paper den nach ihnen benannten Diffie-Hellman-Schlüsselaustausch vorgestellt. Es handelt sich dabei um ein asymmetrisches Verschlüsselungsverfahren. Das grundlegende Prinzip besteht darin, dass sich Kommunikationspartner über einen unsicheren Kanal Nachrichten, aus denen ein gemeinsamer Schlüssel (Shared Secret) berechnet wird, zusenden. Um sich gegen Brute-Force-Angriffe zu schützen, nutzt dieses Public-Key-System das diskrete Logarithmus Problem.
2. Der Algorithmus
- Alphabet: \((\mathbb{Z}_p^{*},\cdot)\).
- Erzeuger: \(g\in(\mathbb{Z}_p^{*},\cdot)\)
- Schlüssel: \(a\) (Alice), \(b\) (Bob).
- Schlüsselaustausch:
1. Alice wählt \(a\in\{1,2,...,p-2\}\) und berechnet \(A=g^a\mod p\)
2. Alice sendet \(A\) an Bob (\(a\) ist der geheime Schlüssel von Alice).
3. Bob wählt \(b\in\{1,2,...,p-2\}\) und berechnet \(B=g^b\mod p\).
4. Bob sendet \(B\) an Alice (\(b\) ist der geheime Schlüssel von Bob).
5. Alice rechnet: \(B^a\mod p=g^{b\cdot a}\) (geheimer Schlüssel für Alice und Bob).
6. Bob rechnet: \(A^b\mod p=g^{b\cdot a}\) (geheimer Schlüssel für Alice und Bob).
7. Der gemeinsame (geheime) Schlüssel ist \(B^a=A^b=g^{a\cdot b} \mod p\).
3. Beispiel
Gegeben sei das Alphabet \((\mathbb{Z}_{107}^{*},\cdot)\) und ein dazugehöriger Erzeuger $5$. Gesucht ist der gemeinsame geheime Schlüssel von Alice und Bob. \(p=107\) und \(g=5\) sind öffentlich. Wir wenden nun den Diffie-Hellman-Schlüsselaustauschalgorithmus Schritt-für-Schritt an:
- Alphabet: \((\mathbb{Z}_{107}^{*},\cdot)\)
- Erzeuger: \(g=5\in(\mathbb{Z}_{107}^{*},\cdot)\)
- Schlüssel: \(a\) (Alice), \(b\) (Bob)
- Schlüsselaustausch:
1. Alice wählt \(a=32\) und berechnet \(A=5^{32}\equiv 83\mod 107\).
2. Alice sendet \(83\) an Bob (\(83\) ist der geheime Schlüssel von Alice).
3. Bob wählt \(b=6\) und berechnet \(B=5^6\equiv 3\mod 107\).
4. Bob sendet \(3\) an Alice (\(3\) ist der geheime Schlüssel von Bob).
5. Alice berechnet: \(3^{32}\equiv 13\mod 107\) (geheimer Schlüssel für Alice und Bob).
6. Alice berechnet: \(83^{6}\equiv 13\mod 107\) (geheimer Schlüssel für Alice und Bob).
7. Der gemeinsame geheime Schlüssel von Alice und Bob ist \(13\).
4. Man-in-the-Middle-Angriff auf Diffie-Hellman
Dieses Verfahren ist nicht gegen Man-in-the-Middle-Angriffe geschützt, da hierdurch die Authentifizierungsnachrichten manipuliert werden können. Dazu fängt ein Angreifer Mallory die Authentifizierungsnachrichten ab und sendet stattdessen
einen eigenen Wert \(M=g^m\mod p\) mit \(m\in\left\{1,2,...,p-2\right\}\) an Alice und Bob.
Der Schlüsselaustausch findet somit nicht mehr zwischen Alice und Bob, sondern zwischen Alice und
Mallory, sowie Bob und Mallory statt. Daraus ergeben sich folgende Schlüssel für einzelnen
Kommunikationspartner:
- Alice: \(k_A=M^a\mod p=g^{m\cdot a}\mod p\)
- Bob: \(k_B=M^b\mod p=g^{m\cdot b}\mod p\)
- Mallory:
1. \(k_A=g^{m\cdot a}\mod p=A^m\mod p\)
2. \(k_B=g^{m\cdot b}\mod p=B^m\mod p\)
Nun liegt eine symmetrisch verschlüsselte Kommunikation vor. Mallory ist im Besitz der Schlüssel für die Ver- und Entschlüsselung der Nachrichten von Alice und Bob. Dies befähigt Mallory dazu, die abgefangenen Nachrichten mit dem Schlüssel des jeweiligen Senders zu entschlüsseln und nach dem Lesen/Manipulieren mit dem Schlüssel des jeweiligen Empfängers wieder zu verschlüsseln und anschließend zu versenden.
Autor: Florian André Dalwigk
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.