Die Lösung von b) kann schon deshalb nicht richtig sein, da die Schleife von 1 nach 3 nach 2 nach 1 zu einem sogenannten Broadcast-Sturm führen würde.
Ich gehe im folgenden davon aus, dass es sich bei dem Protokoll, das den Spanning Tree aufbaut, um das Spanning-Tree-Protocol handelt und nicht z.B. um das RSTP. Ersteres ist sozusagen der 'Klassiker' hat aber den Nachteil, das der gesamte Spanning Tree mit Einschalten des Switches 10 neu aufgebaut wird. So 100% sicher bin ich mir nicht, aber nach allem, was ich weiß, wird der Tree nach dem Anschließen von Switch10 so aussehen:
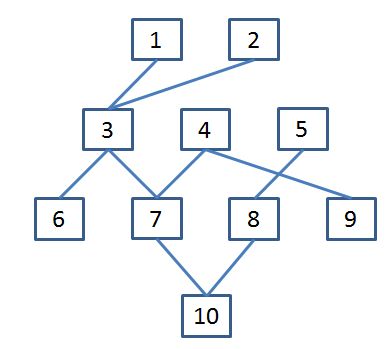
Beim Anschließen wird Switch10 BPDUs verschicken, die von den anderen Switches weiter geleitet werden. Am Ende sollte jeder Switch auf dem kürzesten Weg (der Pfad der geringsten Kosten) mit dem Root-Switch (jetzt Switch10) verbunden sein. Sind zwei Wege gleich lang, so wird er den Switch mit der kleineren MAC-Adresse wählen. In Deiner Lösung ist z.B. Switch9 über 9-5-1-3-7-10 zum Root verbunden. Dabei sind zwei kürzere Verbindungen möglich, nämlich 9-4-7-10 und 9-5-8-10. Da sie gleichwertig sind, wird der Switch9 die Verbindung über Switch4 wählen.
So kannst Du Dir für jeden der Knoten überlegen, was seine optimale - d.h. kostengünstigste - Verbindung zum Switch10 ist. Da alle Verbindungen hier lt. Aufgabenstellung gleichwertig sind, entsprechen die Kosten der Anzahl der Switches auf dem Weg zum Root.
Gruß Werner