Frage:
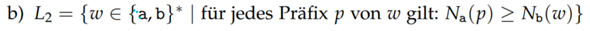
Text erkannt:
b) \( L_{2}=\left\{w \in\{a, b\}^{*} \mid\right. \) für jedes Präfix \( p \) von \( w \) gilt: \( \left.N_{a}(p) \geq N_{b}(w)\right\} \)
Gesucht ist eine kontextfreie Grammatik, die diese Sprache erzeugt.
Meine Idee
G = ( {S} , {a,b} , S , {S --> aSb | aSa | aa | ab | e} )
So ist das Präfix p ∈ {a}* und nicht p ∈ { a , b }*
Könnte mir bitte jemand behilflich sein :(