1. Einführung
In diesem Artikel geht es um die Berechnung von Cronbach's Alpha in dem Statistikprogramm R anhand einer (fiktiven) Depressions-Studie. Das Cronbach's Alpha ist eine bekannte Kennzahl in der empirischen Sozialforschung, die nach Lee J. Cronbach benannt wurde und zur Reliabilitätsprüfung eingesetzt wird. Hierbei wird überprüft, ob die Items zur Messung einer Variablen reliabel sind (die Methode über Cronbach's Alpha bezeichnet man auch als "Reliabilitätsprüfung durch interne Konsistenz"). Cronbach's Alpha kann Werte zwischen \(-\infty\) und (inklusive) \(+1\) annehmen.
Übrigens: Cronbach selbst setzte sich zu Lebzeiten dafür ein, dass diese Kennzahl "Coefficient Alpha" genutzt wird, da seiner Meinung nach bereits viele vor ihm ähnliche Größen vorgeschlagen haben. Schließlich setzte sich jedoch die Bezeichnung "Cronbach's Alpha" durch. In \(80\%\) der Fälle wird Ihnen in der Literatur der Begriff "Cronbach's Alpha begegnen".
2. Installation des R-Zusatzpakets "Psych"
Um Cronbach's Alpha in R berechnen zu können, wird das R-Zusatzpaket psych benötigt. Geben Sie zur Installation des Pakets den folgenden Befehl in die R-Konsole ein:
install.packages("psych")
Nach der Bestätigung durch ENTER werden Sie mit den Worten
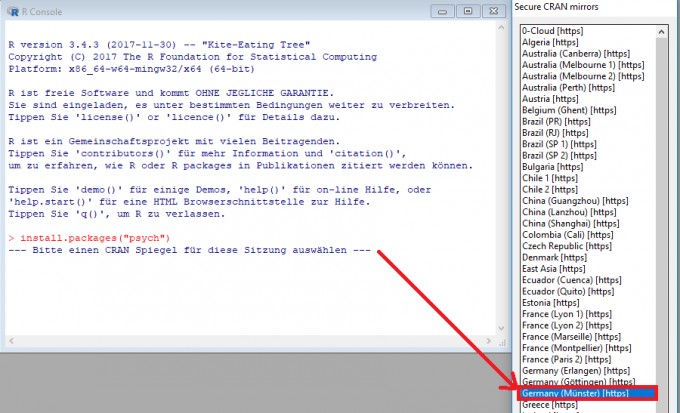
--- Bitte einen CRAN Spiegel für diese Sitzung auswählen ---
von R dazu aufgefordert, einen CRAN-Spiegel (Download-Server) auszuwählen. Sie können dafür den Server Münster (Germany) auswählen. Klicken Sie anschließend auf OK.
Um das installierte Paket nutzen zu können, geben Sie den Befehl
library(psych)
ein und haben Zugriff auf alle Funktionen des Pakets.
3. Die Studie
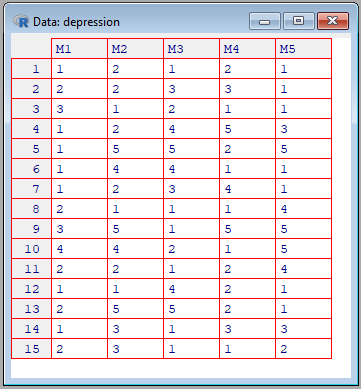
Angenommen, wir haben eine Depressions-Studie mit 15 Teilnehmern durchgeführt, die jeweils 5 Fragen (Items) bearbeiten sollten. Für jede Frage standen dem Teilnehmer 5 Auswahlmöglichkeiten (5-stufige Likert-Skala) zur Verfügung. Die Studie lieferte folgende Ergebnisse:
M1 M2 M3 M4 M5
1 2 1 2 1
2 2 3 3 1
3 1 2 1 1
1 2 4 5 3
1 5 5 2 5
1 4 4 1 1
1 2 3 4 1
2 1 1 1 4
3 5 1 5 5
4 4 2 1 5
2 2 1 2 4
1 1 4 2 1
2 5 5 2 1
1 3 1 3 3
2 3 1 1 2
M1-M5 sind die Items ("Mood1", "Mood2", ..., "Mood5"). Wie können wir daraus Cronbach's Alpha in R berechnen? Zuerst laden wir mit dem Befehl
depression = read.table("C:/Pfad/zur/Datei/drepression.txt", header=TRUE)
die Daten in das Statistikprogramm. Mit View(depression) können wir uns die Tabelle ansehen und überprüfen, ob der Import das gewünschte Ergebnis liefert.
4. Die Berechnung von Cronbach's Alpha
Die Berechnung von Cronbach's Alpha erfolgt mit dem Befehl
alpha(depression[c("M1","M2","M3","M4","M5")], check.keys=TRUE)
Mit der Funktion alpha() wird Cronbach's Alpha berechnet. Mit dem Ausdruck depression[c("M1","M2","M3","M4","M5")] drücken wir aus, dass wir Cronbach's Alpha für die Spalten (Items) "M1","M2","M3","M4" und "M5" in der Tabelle depression berechnen wollen. Das (optionale) Argument check.keys=TRUE sorgt dafür, dass während der Berechnung überprüft wird, ob alle Items gleich gepolt sind (dieser Begriff ist im Kontext der Fragebogenkonstruktion relevant und spielt für diesen Artikel keine wichtige Rolle). Dabei wird ggf. automatisch eine Umpolung vorgenommen.
Als Ergebnis erhalten Sie einen recht umfangreichen Output:
Reliability analysis
Call: alpha(x = depression[c("M1", "M2", "M3", "M4", "M5")], check.keys = TRUE)
raw_alpha std.alpha G6(smc) average_r S/N ase mean sd
0.38 0.43 0.54 0.13 0.77 0.25 2.9 0.77
lower alpha upper 95% confidence boundaries
-0.11 0.38 0.88
Reliability if an item is dropped:
raw_alpha std.alpha G6(smc) average_r S/N alpha se
M1 0.15 0.11 0.30 0.031 0.13 0.35
M2 0.43 0.49 0.49 0.194 0.96 0.24
M3- 0.38 0.42 0.45 0.156 0.74 0.26
M4- 0.48 0.52 0.58 0.212 1.07 0.22
M5 0.11 0.23 0.34 0.071 0.31 0.39
Item statistics
n raw.r std.r r.cor r.drop mean sd
M1 15 0.71 0.77 0.715 0.547 1.8 0.94
M2 15 0.44 0.42 0.252 0.062 2.8 1.47
M3- 15 0.52 0.50 0.361 0.130 3.5 1.55
M4- 15 0.35 0.38 0.081 -0.014 3.7 1.40
M5 15 0.74 0.69 0.620 0.405 2.5 1.68
Non missing response frequency for each item
1 2 3 4 5 miss
M1 0.47 0.33 0.13 0.07 0.00 0
M2 0.20 0.33 0.13 0.13 0.20 0
M3 0.40 0.13 0.13 0.20 0.13 0
M4 0.33 0.33 0.13 0.07 0.13 0
M5 0.47 0.07 0.13 0.13 0.20 0
Warnmeldung:
In alpha(depression[c("M1", "M2", "M3", "M4", "M5")], check.keys = TRUE) :
Some items were negatively correlated with total scale and were automatically reversed.
This is indicated by a negative sign for the variable name.
Wichtig für unsere Überlegungen ist hier die Zeile
raw_alpha std.alpha G6(smc) average_r S/N ase mean sd
0.38 0.43 0.54 0.13 0.77 0.25 2.9 0.77
raw_alpha gibt Cronbach's Alpha an.
5. Interpretation der Ergebnisse
Die folgende Tabelle gibt an, wie die verschiedenen Werte für Cronbach's Alpha zu interpretieren sind.
\(\begin{array}{|l|c|}\hline \alpha\geq 0.9 & \text{Ausgezeichnet}\\\hline 0.8\leq\alpha < 0.9 & \text{Gut}\\\hline 0.7\leq\alpha < 0.8 & \text{Akzeptabel}\\\hline 0.6\leq\alpha < 0.7 & \text{Fragwürdig}\\\hline 0.5\leq\alpha < 0.6 & \text{Schlecht}\\\hline \alpha < 0.5 & \text{Völlig inakzeptabel}\\\hline \end{array}\)
Mit einem Wert von \(0.38\), der völlig inakzeptabel ist, kann darauf geschlossen werden, dass den Fragebogen wohl ein Praktikant erstellt hat, der wenig Ahnung von seinem Fach und/oder Statistik hat ;-)
Autor: Florian André Dalwigk
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.