https://www.youtube.com/watch?v=Z-UQFDC-vVo
1. Einführung
Gegeben sei der folgende nicht-deterministische Automat (kurz NFA bzw. NEA).
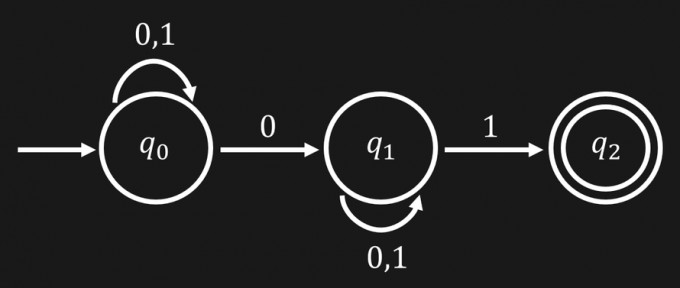
Warum ist das ein NFA? Das liegt z. B. daran, dass im Zustand \(q_0\) nicht eindeutig festgelegt ist, in welchen Zustand man beim Lesen der \(0\) gelangt. Mit der \(0\) kommt man nämlich von \(q_0\) wieder in \(q_0\) oder in \(q_1\).
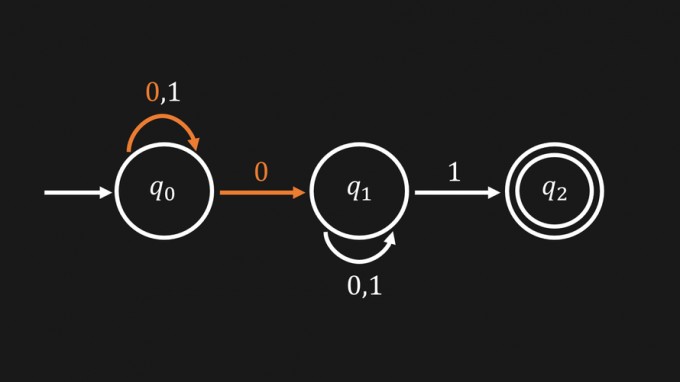
Zudem gelangt man von \(q_1\) mit einer \(1\) entweder wieder in den Zustand \(q_1\) oder in den Zustand \(q_2\).
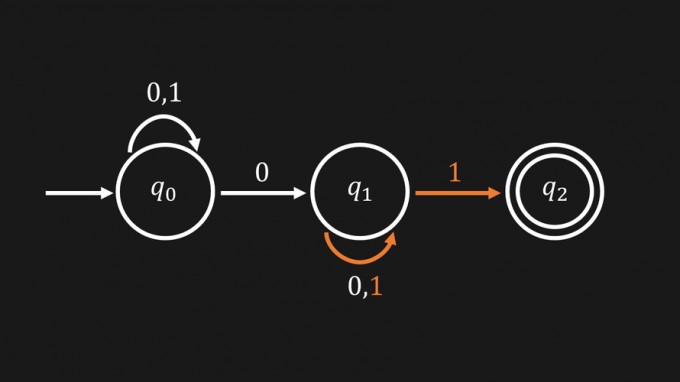
Das Problem bei NFAs ist, dass der Weg, der beim Lesen eines Wortes durch den Automaten genommen wird, nicht eindeutig ist. Dies kann dazu führen, dass man im schlimmsten Fall alle möglichen Pfade ausprobieren muss, um entscheiden zu können, ob ein bestimmtes Wort von dem Automaten akzeptiert wird. Wenn du für den gegebenen Automaten prüfen willst, ob das Wort \(01\) akzeptiert wird, musst du von \(q_0\) mit der \(0\) direkt in \(q_1\) und von \(q_1\) mit der \(1\) direkt in \(q_2\) gehen. Wenn du zuerst von \(q_0\) aus mit der \(0\) wieder in \(q_0\) gehst, kommst du nur über eine weitere \(0\) in \(q_2\). Dieser Pfad zwingt einen quasi dazu, einen alternativen Pfad zu gehen.
Ein deterministischer endlicher Automat (DFA) wäre an dieser Stelle also weitaus hilfreicher, da der Weg durch den Automaten beim Lesen eines Wortes eindeutig ist und sehr schnell entschieden werden kann, ob ein Wort überhaupt akzeptiert wird.
2. Die Potenzmengenkonstruktion
Doch wie genau kann man einen NFA in einen DFA umwandeln? Zunächst einmal die gute Nachricht: Jeder NFA lässt sich durch endlich viele Schritte in einen DFA umwandeln. Das kann man sogar mathematisch beweisen. Es gibt keine Ausnahmefälle, in denen das nicht möglich ist. Das Verfahren, mit dem du die Umwandlung vornehmen kannst und das du gleich kennenlernst, führt potentiell zu einem hohen Berechnungsaufwand. Betrachte dazu den folgenden Automaten:
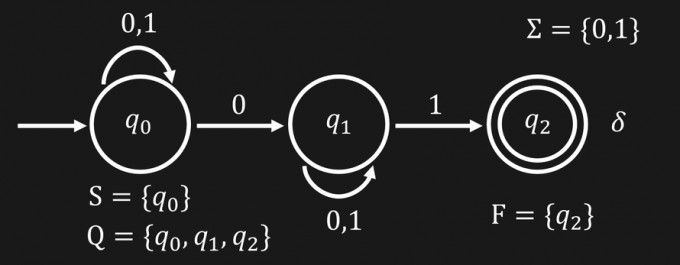
Dieser Automat besitzt als Startzustand \(q_0\). In einem NFA könnten theoretisch auch mehrere Startzustände möglich sein, weshalb an dieser Stelle die Mengenklammern um den Zustand stehen. Das Alphabet besteht aus den Zeichen \(0\) und \(1\). Die Zustandübergangsfunktion \(\delta\) ist bereits durch den Automaten und muss nicht separat aufgeschrieben werden. Der Automat besitzt insgesamt \(3\) Zustände, nämlich \(q_0,q_1\) und \(q_2\). \(q_2\) ist ein Endzustand. Auch bei den Endzuständen gilt, dass es hiervon mehrere geben kann.
Der Algorithmus basiert auf dem mathematischen Begriff der Potenzmenge und wird Potenzmengenkonstruktion genannt.
Definition: Potenzmenge
\(\mathcal{P}(A)\) einer Menge \(A\) ist die Menge, die alle Teilmengen von \(A\) enthält.
Satz: Anzahl der Elemente einer Potenzmenge
Wenn \(A\) eine Elemente mit \(n\) Elementen ist, dann besitzt die Potenzmenge \(\mathcal{P}(A)\) von \(A\) genau $$2^n$$ Elemente.
Wenn eine Menge also \(5\) Elemente besitzt, dann hat ihre Potenzmenge \(2^5=32\) Elemente. Die Anzahl der Elemente in der Potenzmenge steigt also exponentiell.
Von was wird in dem Algorithmus die Potenzmenge gebildet? Ganz einfach! Von den Zuständen in dem Automaten. Heißt das, dass bei einem Automaten mit \(3\) Zuständen bereits \(2^3=8\) Zustände während des Algorithmus erzeugt werden müssen? Nein! Jedenfalls nicht, wenn wir (wie gleich gezeigt) systematisch vorgehen und nur die Teilmengen an Zuständen konstruieren, die wir tatsächlich benötigen.
Du wirst die Funktionsweise des Algorithmus nun an einem konkreten Beispiel kennenlernen.
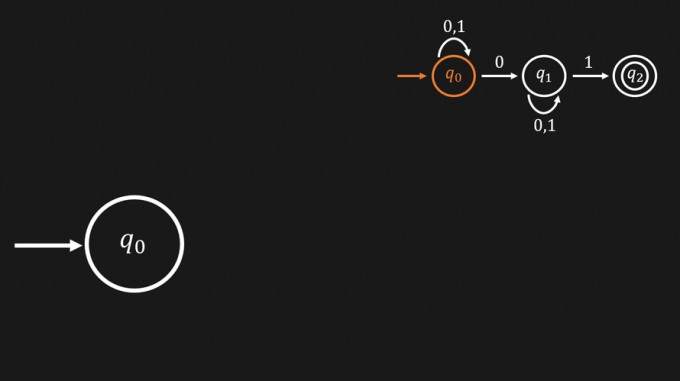
Du beginnst bei einem der Startzustände (in diesem Fall gibt es nur einen) und dringst über die einzelnen Zeichen in andere Zustände vor.
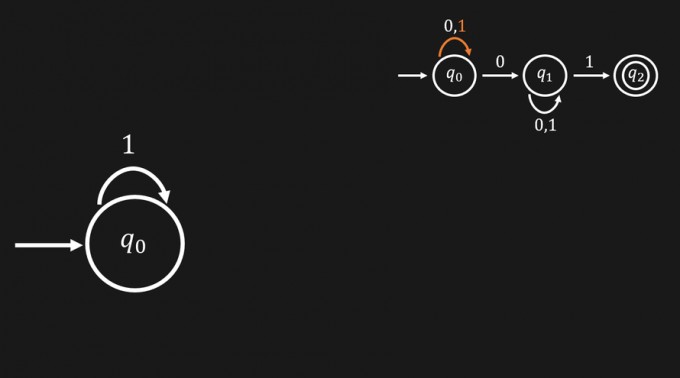
Du prüfst für jedes Zeichen aus dem Alphabet, in welchen Zustand man von dem aktuell betrachteten Zustand aus landet. Vom Startzustand aus landest du mit der \(1\) wieder in Zustand \(1\).
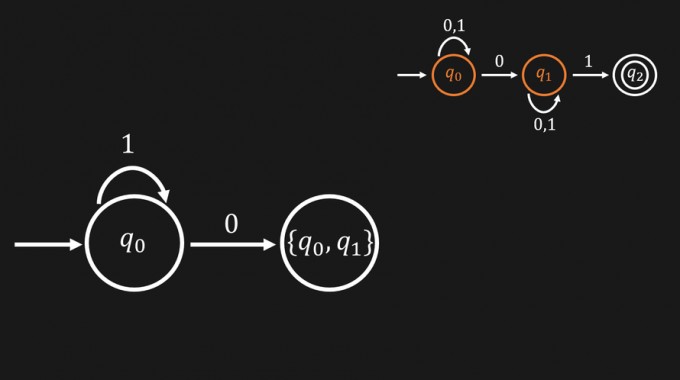
Mit der \(0\) landest du vom Startzustand aus allerdings entweder in \(q_0\) oder in \(q_1\). D. h. wir packen diese beiden Zustände in einen neuen Zustand, den wir \(\{q_0,q_1\}\) nennen. Das ist jetzt eine Teilmenge aus der Menge aller Zustände und somit ein Element der Potenzmenge aller Zustände.
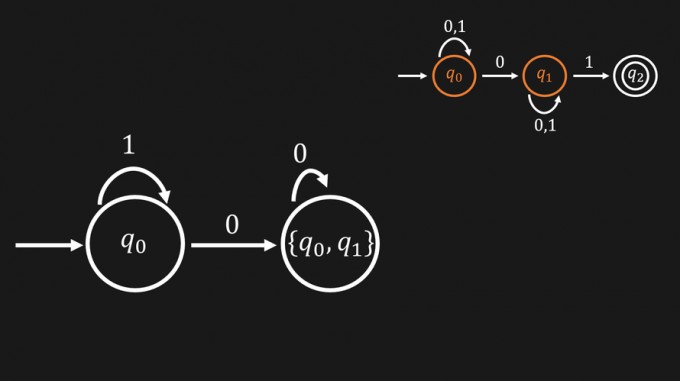
Statt alle möglichen Teilmengen der Zustandsmenge zu bilden und dann zu entscheiden, welche benötigt wird, kannst du so sukzessive vorgehen. Nun gehst du von dem Zustand \(\{q_0,q_1\}\) aus und prüfst, in welche Zustände du mit den Zeichen \(0\) und \(1\) kommst. Hierzu schaust du für jeden der Zustände \(q_0\) und \(q_1\), in welchen Zustand du mit ihnen in dem ursprünglichen Automaten kommst. Mit der \(0\) kommst du von \(q_0\) in \(q_0\) oder \(q_1\) und von \(q_1\) wieder in \(q_1\).
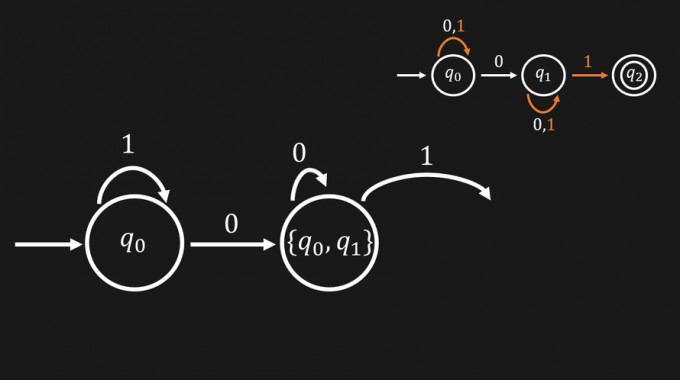
Du kommst insgesamt also von dem Zustand \(\{q_0,q_1\}\), der quasi aus den ursprünglichen Zuständen \(q_0\) und \(q_1\) besteht, wieder in \(\{q_0,q_1\}\). Wenn das noch etwas verwirrend klingt, wirst du beim nächsten Schritt sehen, wie das gemeint ist. Wenn du nämlich eine \(1\) liest, dann kommst du vom Zustand \(q_0\) wieder in den Zustand \(q_0\), sowie von dem Zustand \(q_1\) wieder in den Zustand \(q_1\) und zusätzlich von dem Zustand \(q_1\) in den Zustand \(q_2\). D. h. du erreichst vom Zustand \(\{q_0,q_1\}\) insgesamt \(3\) Zustände, nämlich \(q_0,q_1\) und \(q_2\).
WEITERE BILDER FOLGEN (zu viele Uploads)
Diese fasst du zu einem neuen Zustand \(\{q_0,q_1,q_2\}\) zusammen.
WEITERE BILDER FOLGEN (zu viele Uploads)
Warum ist dieser Zustand umkreist (also als akzeptierender Zustand markiert)? Das liegt daran, dass immer dann, wenn in einem "neuen" Zustand ein akzeptierender Zustand des ursprünglichen Automaten steht, dieser "neue" Zustand dann auch akzeptierend ist.
Jetzt musst du für den neu hinzugekommenen Zustand \(\{q_0,q_1,q_2\}\) erneut prüfen, in welche Zustände du beim Lesen aller Zeichen aus dem Alphabet \(\Sigma\) von diesem Zustand aus gelangst. Von \(q_0\) gelangst du mit einer \(0\) wieder in den Zustand \(q_0\) oder \(q_1\) und von \(q_1\) aus gelangst du mit einer \(0\) wieder in \(q_1\).
WEITERE BILDER FOLGEN (zu viele Uploads)
Insgesamt gelangst du mit einer \(0\) also wieder in den Zustand \(\{q_0,q_1\}\).
Mit einer \(1\) gelangst du vom Zustand \(q_0\) wieder in \(q_0\), von \(q_1\) in den Zustand \(q_1\) oder \(q_2\) und von \(q_2\) nirgendwo hin. Vom Zustand \(\{q_0,q_1,q_2\}\) gelangst du mit einer \(1\) also wieder in den Zustand \(\{q_0,q_1,q_2\}\).
WEITERE BILDER FOLGEN (zu viele Uploads)
Da jetzt für jeden Zustand klar ist, wo man mit einer \(1\) und einer \(0\) hinkommt, ist der Algorithmus an dieser Stelle beendet und der NFA erfolgreich in einen DFA überführt worden. Ob du den Algorithmus korrekt angewendet hast, kannst du mit ein paar kleinen Tests überprüfen, indem du dir ein Wort ausdenkst und prüfst, ob es von beiden Automaten akzeptiert oder von beiden nicht akzeptiert wird. Stimmen die Ergebnisse beider Automaten überein, liegst du vermutlich richtig. Um ganz sicher zu gehen, müsstest du jedoch alle Fälle ausprobieren, was allerdings aufgrund der unendlich vielen Möglichkeiten nicht funktioniert.
Dieser Automat ist übrigens nicht zwangsläufig schon minimal. Dafür kannst du dir mein Video zum Minimieren von Automaten ansehen.
Autor: Florian André Dalwigk
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.