a) Beim Scheduling via Round Robin werden alle Prozesse zunächst in eine Queue eingereiht und jedem Prozess ein Quantum zugeteilt (hier allen Prozessen \(3\)ms). Gemäß der Reihenfolge in der Queue wird den Prozessen die CPU zugewiesen. Wenn ein Prozess nach Ablauf seines Quantums noch im Zustand "running" ist, wird ihm die CPU entzogen und er wechselt seinen State zu "ready". Anschließend wird er ans Ende der Queue verlegt und der erste Prozess in der Warteschlange erhält die CPU. Die Wahl des Quantums sollte sinnvoll sein. Das ist genau dann der Fall, wenn das Verhältnis zwischen Quantum und der Zeit, die das System für einen Context Switch benötigt, vernünftig ist. Wird das Quantum zu groß gewählt, so ist das zwar ein effizienter Ansatz, allerdings muss man ggf. mit langen Verzögerungs- und Wartezeiten rechnen (darauf zielt glaube ich auch die b) ab). Bei einem zu kleinen Quantum hat man wiederum sehr kurze Antwortzeiten, doch aufgrund der häufigen Prozessumschaltungen einen großen Overhead. Ich denke, dass \(3\)ms in Ordnung sind. So weit zur Theorie um den Algorithmus. Beschäftigen wir uns nun mit dem Beispiel.
Am Anfang enthält die Queue \(P_1\), der eine Rechenzeit von \(10\)ms benötigt. Diesem wird direkt die CPU zugeteilt.
Nach einer Millisekunde kommt \(P_2\) in die Queue. Zu diesem Zeitpunkt hat \(P_1\) bereits eine Millisekunde gerechnet. Danach kommt \(P_3\) in die Queue und wird hinter \(P_2\) eingereiht. Zu diesem Zeitpunkt hat \(P_1\) bereits \(2\)ms gerechnet. Nun kommt auch der letzte Prozess \(P_4\) hinzu, der hinter \(P_3\) in der Queue positioniert wird:
\(\begin{array}{|c|c|} \hline \text{Prozess} & \text{Rechenzeit [ms]} & \text{verbleibende Rechenzeit [ms]}\\\hline P_1 & 10 & 7\\\hline P_2 & 4 & 4\\\hline P_3 & 5 & 5\\\hline P_4 & 3 & 3\\\hline\end{array}\)
Da \(P_1\) sein Quantum aufgebraucht hat und noch nicht fertig ist, wird er hinter \(P_4\) eingereiht und \(P_2\) erhält die CPU. \(P_2\) rechnet \(3\)ms und wird vom Scheduler anschließend hinter \(P_1\) eingeordnet, da auch \(P_2\) nach Aufbrauchen des Quantums noch nicht fertig ist. Nun wird \(P_3\) die CPU zugeteilt, \(3\)ms gerechnet und \(P_3\) danach hinter \(P_2\) eingereiht. Jetzt erhält \(P_2\) die CPU und wird komplett abgearbeitet. \(P_2\) wird also nicht mehr in die Queue geschickt:
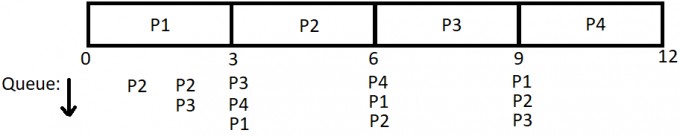
\(\begin{array}{|c|c|} \hline \text{Prozess} & \text{Rechenzeit [ms]} & \text{verbleibende Rechenzeit [ms]}\\\hline P_1 & 10 & 7\\\hline P_2 & 4 & 1\\\hline P_3 & 5 & 2\\\hline P_4 & 3 & 0\\\hline\end{array}\)
Jetzt startet \(P_1\) und arbeitet wieder \(3\)ms. Nach der Abarbeitung wird \(P_1\) hinter \(P_3\) positioniert. Den Prozessen \(P_2\) und \(P_3\) wird nun nacheinander die CPU zugeteilt. Beide werden komplett fertig (und benötigen dafür nicht einmal ihr gesamtes Quantum).

\(\begin{array}{|c|c|} \hline \text{Prozess} & \text{Rechenzeit [ms]} & \text{verbleibende Rechenzeit [ms]}\\\hline P_1 & 10 & 4\\\hline P_2 & 4 & 0\\\hline P_3 & 5 & 0\\\hline P_4 & 3 & 0\\\hline\end{array}\)
Nun wird \(P_1\) abgearbeitet:
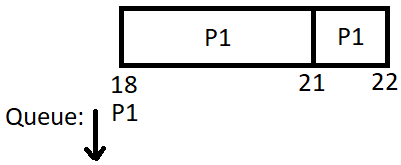
\(\begin{array}{|c|c|} \hline \text{Prozess} & \text{Rechenzeit [ms]} & \text{verbleibende Rechenzeit [ms]}\\\hline P_1 & 10 & 1\\\hline P_2 & 4 & 0\\\hline P_3 & 5 & 0\\\hline P_4 & 3 & 0\\\hline\end{array}\)
\(\begin{array}{|c|c|} \hline \text{Prozess} & \text{Rechenzeit [ms]} & \text{verbleibende Rechenzeit [ms]}\\\hline P_1 & 10 & 0\\\hline P_2 & 4 & 0\\\hline P_3 & 5 & 0\\\hline P_4 & 3 & 0\\\hline\end{array}\)
b) Bei FIFO (bzw. FCFS, "First come, first served") erhält ein ankommender Prozess so lange die CPU, bis er abgearbeitet wurde. Wenn wir uns also das Maximum der angegebenen Rechenzeiten heraussuchen und das als Quantum wählen, können alle Prozesse komplett abgearbeitet werden. Deswegen sollte bei einem Quantum von \(10\)ms das Verhalten dem von FIFO ähneln. Auf diese Weise wird Prozess \(P_1\) nicht unterbrochen (die anderen haben ohnehin eine geringere Rechenzeit).