Kontextfreie Grammatiken erstellen aus Definitionen von Sprachen: Könnten meine Lösungen stimmen?

Question

Aufgabe:

Erstellen Sie kontextfreie Grammatiken für die folgenden Sprachen. Das Alphabet ist jeweils Σ = {0, 1}
a) L = {w ∈ {0, 1}∗ | w enthält das Teilwort 0 und die Länge von w ist ungerade}
b) L = {w ∈ {0, 1}∗ | w enthält das Teilwort 11 und die Länge von w ist gerade}
c)  L = { w | die Länge von w ist ungerade und das Symbol in der Mitte ist eine 1 }

Problem/Ansatz:

Könnten meine Lösungen auch stimmen?
a)

Text erkannt:

\( \begin{array}{rl}G: & (\mathbb{\Sigma}, P, S) \quad \Sigma=\{0,1\} \quad N=\{S, A, B\} \\ & S \longrightarrow A A O|O A A| A O A \mid O \\ & \longrightarrow B O|B 1| 0 \mid 1 \\ B & O O|O 1| 10 \mid 11\end{array} \)

b)

Text erkannt:

\( \mathcal{C}:=(N, \Sigma, P, S) \quad \Sigma=\{0,1\} \quad \mathbb{R} N=\{\}, A, B\} \)
\( S \rightarrow 11|11 \mathrm{AA} \eta \mathrm{AA} 11| \mathrm{A} 11 \mathrm{~A} \)
\( A \rightarrow O B|\wedge B| 011 \)
\( B \rightarrow O 0|O 1| 10 \mid 11(0 B \mid 1 B \)

c)

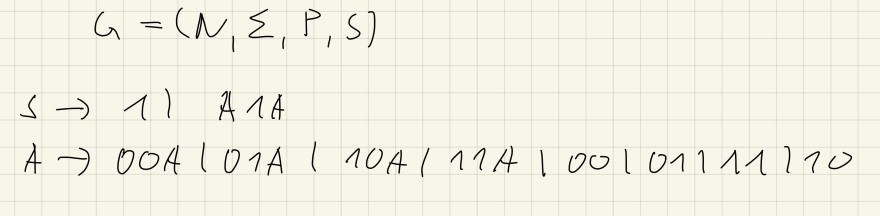
Text erkannt:

\( \begin{aligned} & G=(N, \Sigma, P, S) \\ S \rightarrow &1) A 1 A \\ A \rightarrow &O O A|O 1 A| 10 A|11 A| 00 \mid 01111) 10 \end{aligned} \)

Answer 1

a) Das Wort \(111101111\) kann nicht abgeleitet werden obwohl \(111101111\in L\) ist. Grund dafür ist, dass nur Wörter bis zu einer Länge von 7 abgeleitet werden können.

Deine Vorschläge für b) und c) leiden unter ähnlichen Problemen.

Comments

Danke vielmals Oswald. Hätten Sie mir einen Trick, wie ich solche Regel bestimmen könnte oder wie man hier vorgeht?

Ich bin ein bisschen verloren, bei solchen Aufgaben.

---

Meine Strategie ist R̶u̶m̶ ̶p̶r̶o̶b̶i̶e̶r̶e̶n̶ rumprobieren.