Induktion - Informatik

Question

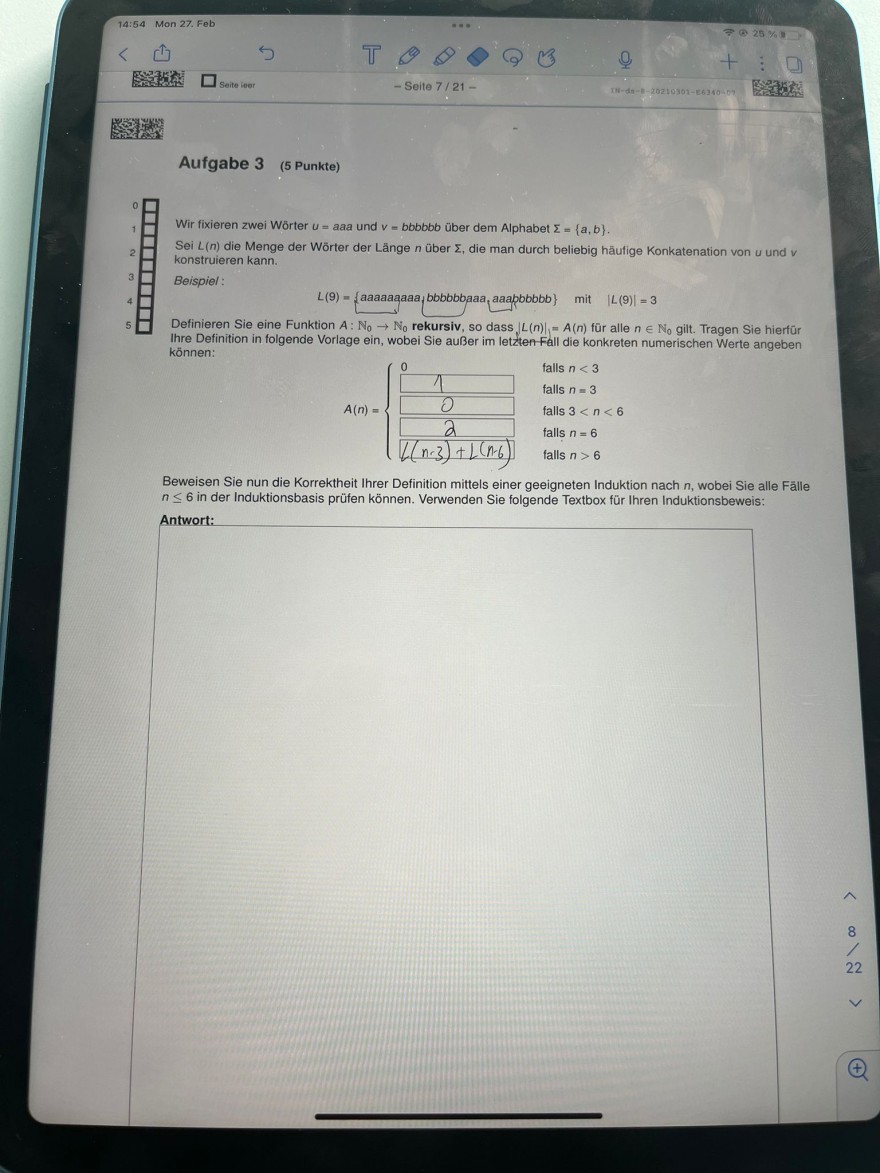
Text erkannt:

Aufgabe 3
(5 Punkte)
Wir fixieren zwei Wörter \( u=a a a \) und \( v=b b b b b b \) über dem Alphabet \( \Sigma=\{a, b\} \).
Sei \( L(n) \) die Menge der Wörter der Länge \( n \) über \( \Sigma \), die man durch beliebig häufige Konkatenation von u und \( v \) konstruieren kann.
Beispiel :
\( L(9)=\{\text { aaaaaaaa }, \text { bbbbbbaaa, } a a a p b b b b b\} \text { mit }|L(9)|=3 \)
Definieren Sie eine Funktion \( A: \mathbb{N}_{0} \rightarrow \mathbb{N}_{0} \) rekursiv, so dass \( |L(n)|=A(n) \) für alle \( n \in \mathbb{N}_{0} \) gilt. Tragen Sie hierfür Ihre Definition in folgende Vorlage ein, wobei Sie außer im letzten Fall die konkreten numerischen Werte angeben können:
\( A(n)=\left\{\begin{array}{l} \frac{0}{\square} \\ \frac{1}{\hline 2} \\ \frac{2}{L(n-3)+L(n-6)} \end{array}\right. \)
falls \( n<3 \)
falls \( n=3 \)
falls \( 3<n<6 \)
falls \( n=6 \)
falls \( n>6 \)
Beweisen Sie nun die Korrektheit Ihrer Definition mittels einer geeigneten Induktion nach \( n \), wobei Sie alle Fälle \( n \leq 6 \) in der Induktionsbasis prüfen können. Verwenden Sie folgende Textbox für Ihren Induktionsbeweis:
Antwort:

Wie soll ich dann meine Definition durch Induktion zeigen?

Außerdem, sollte L(n = 0) nicht 1 ergeben, damit auch der Induktionbasis stimmen kann?

Answer 1

Wie soll ich dann meine Definition durch Induktion zeigen?

Überhaupt nicht. Deine Definition ist falsch. \(A(n)\) ist eine natürliche Zahl. \(L(n-3)\) und \(L(n-6)\) sind Mengen von Wörtern über dem Alphabet \(\{a,b\}\). Das ist ein deutliches Zeichen, dass \(A(n) = L(n-3)+L(n-6)\) nicht sein kann.

Stattdessen:

Sei \(n > 6\).

Sei

        \(A(m) =\begin{cases} 0& \text{falls } m < 3\\ 1& \text{falls } m = 3\\ 0& \text{falls } 3 < m < 6\\ 2& \text{falls } m = 6\\ A(m-3)+A(m-6)& \text{falls } m > 6 \end{cases}\)

für alle \(m < n\).

Zeige, dass \(A(n) = A(n-3)+A(n-6)\) ist.

Das könntest du zum Beispiel zeigen indem du zeigst dass es eine bijektive Abbildung \(L(n)\to L(n-3)\cup L(n-6)\) gibt.

Außerdem, sollte L(n = 0) nicht 1 ergeben

Anscheinend wird das leere Wort nicht als Wort angesehen.

"L(n=0)" ist auch eine etwas ungewöhnliche Schreibweise. Normalerweise schreibt man einfach "L(0)".