Aufgabenstellung:
Gegeben sei der DFA \( M=\left(\{0,1\},\left\{z_{0}, \ldots, z_{4}\right\}, z_{0}, \delta,\left\{z_{0}, z_{4}\right\}\right) \) mit \( \delta \) wie folgt:
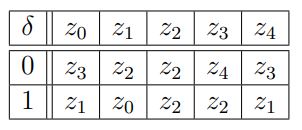
Bereits bearbeitet:
(a) Bestimmen Sie mit dem Algorithmus der Vorlesung den Minimalautomaten \( M^{\prime} \) zu M.
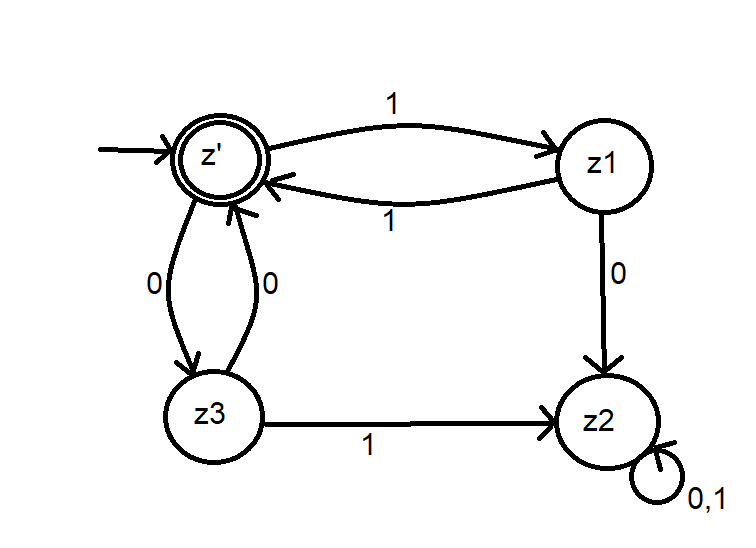
Aufgabe/Problem:
(b) Bestimmen Sie die Äquivalenzklassen der Myhill-Nerode-Relation zu \( M^{\prime} \). Sie müssen nicht die Teilsprachen der Klassen formal charakterisieren, es reicht aus, einen Repräsentanten anzugeben.
Ich verstehe, glaube ich zumindest, was diese Äquivalenzklassen sein sollen, bin mir jedoch nicht sicher und habe keine Ahnung wie ich das aufschreiben soll.