Los Turingmaschine:
Könnte sich jemand meine Lösung zur Aufgabe a20 angucken? Vielen Dank
Text erkannt:
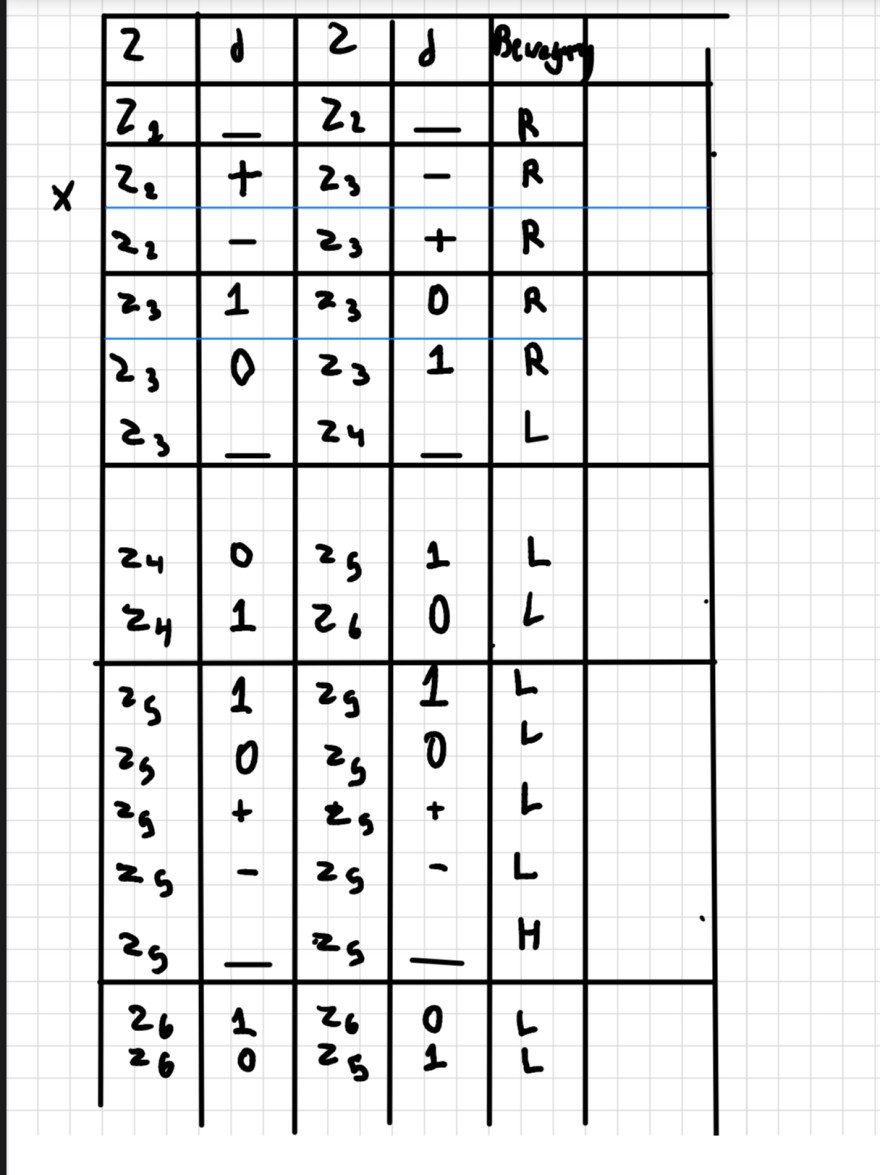
\( \times \)\begin{tabular}{|l|l|l|l|l|l|}
\hline\( z^{2} \) & \( d \) & \( z_{1} \) & \( d \) & \( B_{\text {evay }} \) \\
\hline\( z_{2} \) & - & \( z_{2} \) & - & \( R \) \\
\hline\( z_{2} \) & + & \( z_{3} \) & - & \( R \) & \\
\hline\( z_{2} \) & - & \( z_{3} \) & + & \( R \) & \\
\hline\( z_{3} \) & 1 & \( z_{3} \) & 0 & \( R \) & \\
\hline\( z_{3} \) & 0 & \( z_{3} \) & 1 & \( R \) & \\
\( z_{3} \) & - & \( z_{4} \) & - & \( L \) & \\
\hline\( z_{4} \) & 0 & \( z_{5} \) & 1 & \( L \) & \\
\( z_{4} \) & 1 & \( z_{6} \) & 0 & \( L \) & \\
\hline\( z_{5} \) & 1 & \( z_{9} \) & 1 & \( L \) & \\
\( z_{5} \) & 0 & \( z_{5} \) & 0 & \( L \) & \\
\( z_{9} \) & + & \( z_{5} \) & + & \( L \) & \\
\( z_{5} \) & - & \( z_{5} \) & - & \( L \) & \\
\( z_{5} \) & - & \( z_{5} \) & - & \( H \) & \\
\hline\( z_{6} \) & 1 & \( z_{6} \) & 0 & \( L \) & \\
\( z_{6} \) & 0 & \( z_{5} \) & 1 & \( L \) & \\
\end{tabular}

Text erkannt:
Aufgabe A-20 (Turingmaschinen, Zweierkomplement)
(4 Punkte)
Entwerfen Sie eine Turingmaschine \( \mathcal{T}=\left(Z, \Sigma, \Gamma, \delta, z_{1,-}\right) \) zur Lösung des folgenden Problems. Geben Sie dazu die Zustandsmenge \( Z \), den Anfangszustand \( z_{1} \), das Eingabealphabet \( \Sigma \), das Bandalphabet \( \Gamma \) sowie die Übergangstabelle an. Zu Beginn und am Ende soll der Lese-Schreib-Kopf vor dem ersten Zeichen der Eingabe bzw. Ausgabe stehen. Kommentieren Sie die Bedeutung der einzelnen Zustände bzw. Übergänge.
Eine auf dem Band vorgegebene ganze Zahl in Zweierkomplementdarstellung soll mit ( -1 ) multipliziert werden. Dabei soll die ursprüngliche Zahl mit dem Ergebnis (wiederum in Zweierkomplementdarstellung) überschrieben werden.