Sie sollen mithilfe eines auf PLA basierenden PROM (Programmable Read-Only Memory) die folgenden vier 8-BitWorte speichern, die dann jeweils anhand von 2 Bits adressiert werden sollen.
Adresse
| Wort
|
00
| 01010101
|
01
| 10101010
|
10
| 11111111
|
11
| 00001111
|
a)Wie groß muss das PLA, das Sie verwenden, mindestens sein? Geben Sie die Mindestzahl an Zeilen und an Spalten an.
b)Zeichnen Sie das PLA und spezifizieren Sie den Bausteintyp in jeder Zelle. Vermerken Sie jeweils, welche Zeile /Spalte welche Bedeutung hat.
Ansatz:
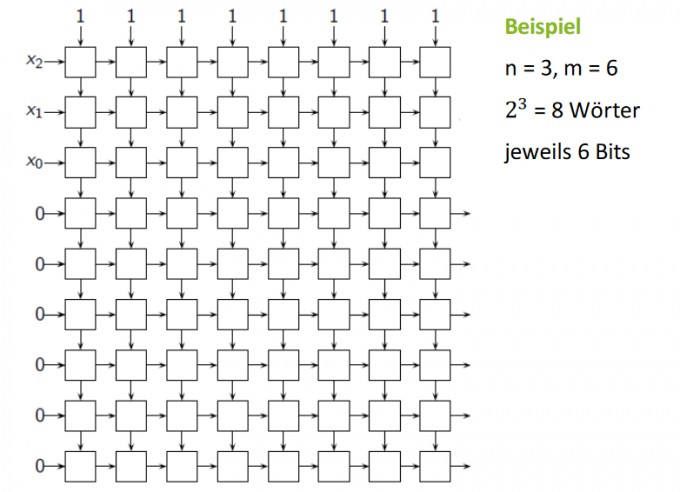
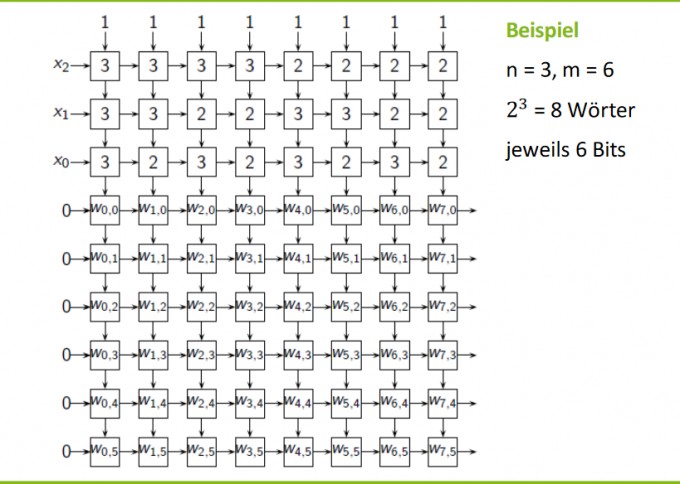
Mein Ansatz wäre es, ungefähr so wie in den unten angegebenen bildern vorzugehen. Leider verstehe ich den Ablauf der verschiedenen schritte in den Bildern nicht ganz.
Text erkannt:
7.4 PLA als Speicher PLA als ROM Aufgabe: Speichere \( 2^{n}, \) Wörter " der Länge m. \[ \begin{aligned} \mathrm{w}_{0}=& \mathrm{w}_{0,0} \mathrm{w}_{0,1} \mathrm{w}_{0,2} \cdots \mathrm{w}_{0, \mathrm{m}-1} \in\{0,1\}^{m} \\ \mathrm{w}_{1}=& \mathrm{w}_{1,0} \mathrm{w}_{1,1} \mathrm{w}_{1,2} \cdots \mathrm{w}_{1, \mathrm{m}-1} \in\{0,1\}^{m} \\ \mathrm{w}_{2}=& \mathrm{w}_{2,0} \mathrm{w}_{2,1} \mathrm{w}_{2,2} \cdots \mathrm{w}_{2, \mathrm{m}-1} \in\{0,1\}^{m} \\ \vdots & \vdots & \vdots \\ \mathrm{w}_{2}^{\mathrm{n}}-1 &=\mathrm{w}_{2}^{\mathrm{n}}-1,0 \mathrm{w}_{2}^{\mathrm{n}}-1,1^{\mathrm{n}}-1,2^{\mathrm{n}}-1,2^{\mathrm{n}} \cdots \mathrm{w}_{2}^{\mathrm{n}}-1, \mathrm{m}-1 \in\{0,1\}^{\mathrm{m}} \end{aligned} \] Benutze \( \quad \) PLA mit \( n+ \) m Zeilen, \( 2^{n} \) Spalten Beobachtung \( \quad \mathrm{m} \cdot 2^{n} \) Zellen für \( \mathrm{m} \cdot 2^{n} \) zu speichernde Bits mindestens erforderlich Adressierung \( \quad \) mit jeweils n Bits in n zusätzlichen Zeilen TU "dentished dectristed