Frage:

Text erkannt:
\begin{tabular}{l|l|l|l|l|}
\hline \( \mathbf{p} \) & \( \mathbf{q} \) & \( \neg q \) & \( p \vee \neg q \) & \( (p \vee \neg q) \Rightarrow q \) \\
\hline T & T & F & T & T \\
\hline T & F & T & T & F \\
\hline F & T & F & F & T \\
\hline F & F & T & T & T \\
\hline
\end{tabular}
Hey Leute, könnt ihr schauen, ob die Wahrheitstabelle richtig ist?
Ich verstehe nicht, warum die letze Spalte T ist also wenn p ∨¬q = T ist und q f ist, wieso ist dann die Implikation
(p∨¬q)⇒q T ?
Diese Tabelle hat mich verwirt:
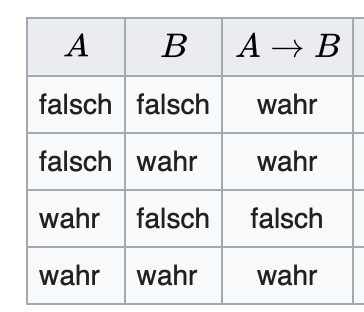
Text erkannt:
\begin{tabular}{|c|c|c|}
\hline\( A \) & \( B \) & \( A \rightarrow B \) \\
\hline falsch & falsch & wahr \\
\hline falsch & wahr & wahr \\
\hline wahr & falsch & falsch \\
\hline wahr & wahr & wahr \\
\hline
\end{tabular}
Code: