Aufgabe:
Geben Sie für die folgenden Sprachen über dem Alphabet \( \{a, b\} \) Automaten an:
1. \( \left\{w \mid w \in\{a, b\}^{*}, w\right. \) enthält mindestens 1 a und mindestens \( \left.1 b\right\} \)
2. \( \left\{w \mid w \in\{a, b, c\}^{*} \text {, jedes } a \text { in } w \text { folgt unmittelbar auf ein } b \text { oder } c\right\}^{1} \)
3. \( \left\{w \mid w \in\{a, b\}^{*}\right. \), die Anzahl a's insgesamt in \( w \) ist ein Vielfaches von 2 , und \( b \) 's treten immer nur in Gruppen mit gerader Anzahl von b's auf \( \}^{2} \)
Problem/Ansatz:
Ich wollte fragen, ob meine Lösung für die 1. richtig ist und ob mir jemand bei den anderen beiden helfen kann.
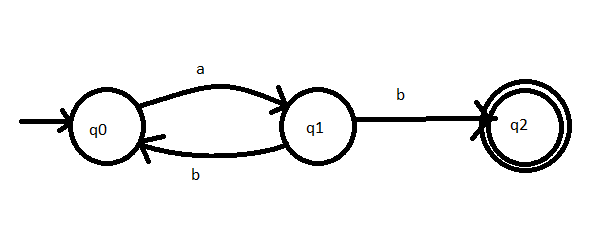
Text erkannt:
\( -0<0-0 \)