Aufgabe:
Text erkannt:
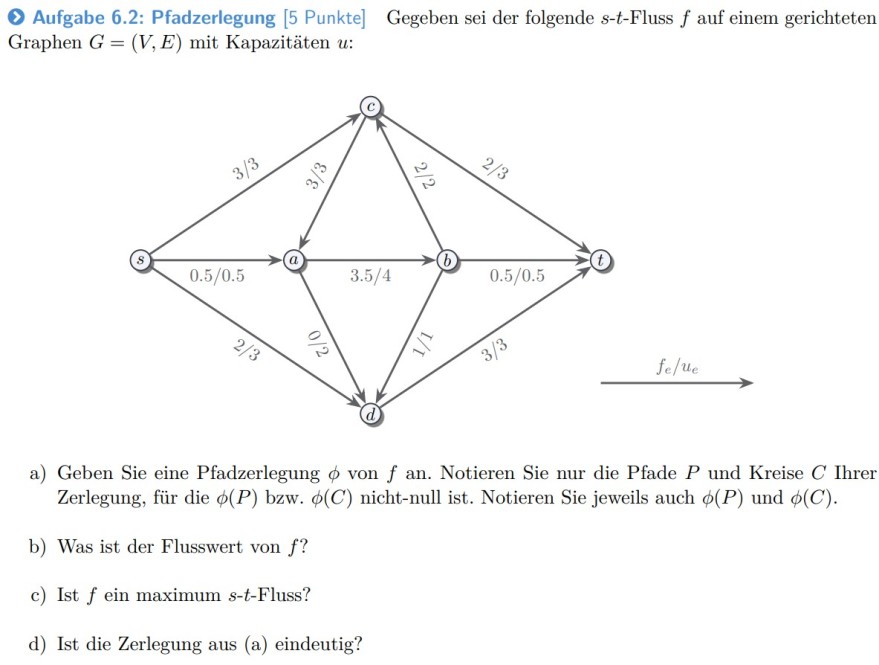
(7) Aufgabe 6.2: Pfadzerlegung [5 Punkte] Gegeben sei der folgende \( s \)-t-Fluss \( f \) auf einem gerichteten Graphen \( G=(V, E) \) mit Kapazitäten \( u \) :
a) Geben Sie eine Pfadzerlegung \( \phi \) von \( f \) an. Notieren Sie nur die Pfade \( P \) und Kreise \( C \) Ihrer Zerlegung, für die \( \phi(P) \) bzw. \( \phi(C) \) nicht-null ist. Notieren Sie jeweils auch \( \phi(P) \) und \( \phi(C) \).
b) Was ist der Flusswert von \( f \) ?
c) Ist \( f \) ein maximum \( s \)-t-Fluss?
d) Ist die Zerlegung aus (a) eindeutig?
Problem/Ansatz:
Ich bin mir unsicher, was in a) von mir verlangt wird. Soll ich jetzt jeden Pfad, der von s zu t möglich ist angeben und den Kreis, also so:
P1: s → a → b → t
P2: s → a → b → c → t
P3: s → a → d → t
P4: s → c → t
P5: s → a → b → d → t
P6: s → c → a → d → t
P7: s → c → a → b → t
P8: s → c → a → b → d → t
P9: s → d → t
C1: a → b → c → a
Und wie soll ich dann Φ für diese Pfade angeben? Müsste ich zum Beispiel für "s → a → b → t" einfach nach der kleinsten Kante suchen, also 0,5? Wenn ja, muss ich dann für den Flusswert von f alle Ergebnisse aus a) summieren???